The Range Density Estimation Task
We consider an autoregressive model trained on a high-dimensional discrete dataset. Range density queries require the following probability: $$p_\theta(X_1 \in R_1, \dots, X_n \in R_n)$$where each region $R_i$ is a subset of variable $i$'s domain.
Example: database queries. SQL queries often contain such range/region constraints on columns. Here's an example query on a personnel database:
SELECT * FROM personnel
WHERE salary > 5000
AND age = 28
This corresponds to $p_\theta(\text{salary} > 5000, \text{age} = 28)$, possibly leaving out unconstrained variables. Database optimizers require these estimates to make queries go fast.
Other applications. In the paper, we show this task is important for another application, text pattern matching: e.g., what's the match probability of .*icml.* in a corpus?
Approximate inference and unconstrained variables. Exact inference of the range query incurs an exponential cost. Naru (VLDB 2020) instead adapts forward sampling to perform approximate inference (Algorithm 1).
Our insight is to exploit the inherent sparsity in queries: they often access just a few columns out of many in the dataset (e.g., imagine education, city, zip in the above database, which are unconstrained). Such variables should not unnecessarily contribute to the cost of the sampling-based approximate inference.
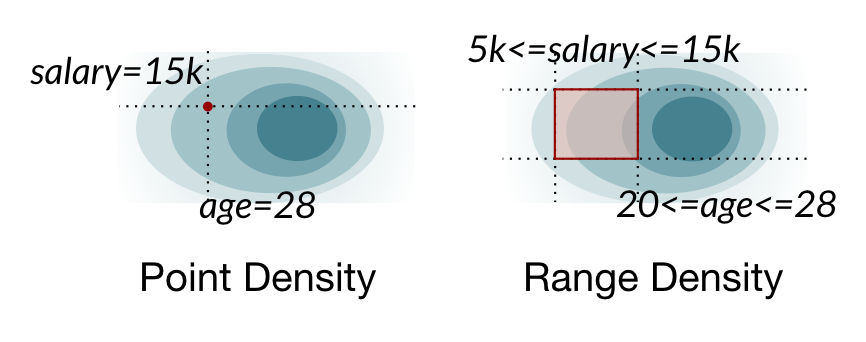 Point vs. range density estimation. Naive marginalization to estimate range densities takes time exponential in the number of dimensions of the joint distribution.
Point vs. range density estimation. Naive marginalization to estimate range densities takes time exponential in the number of dimensions of the joint distribution.
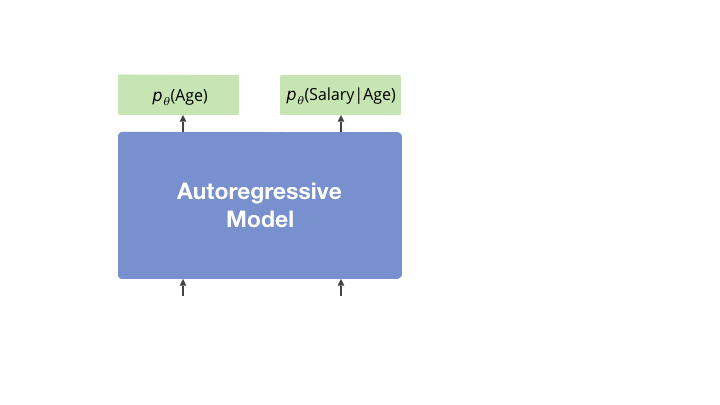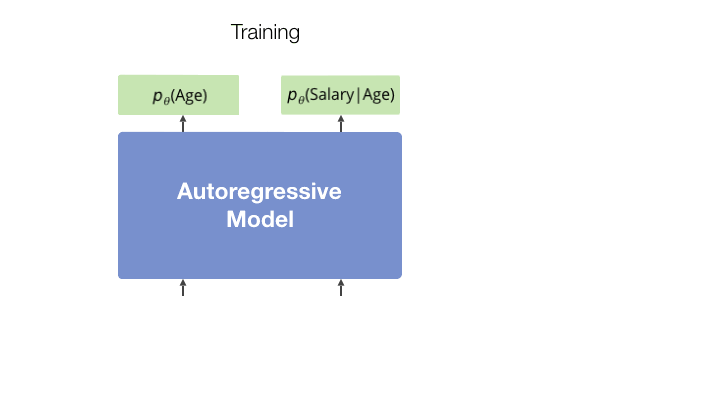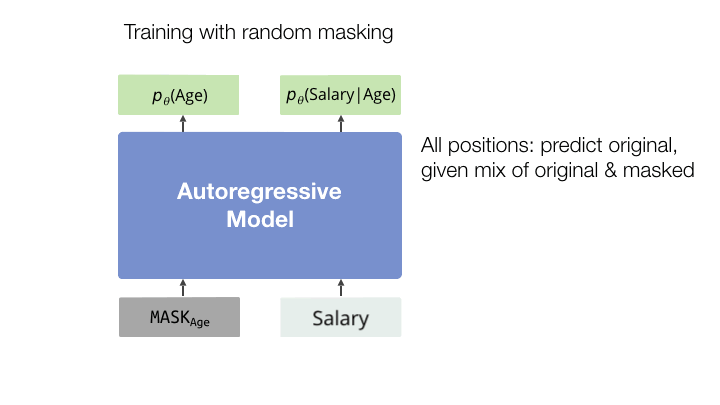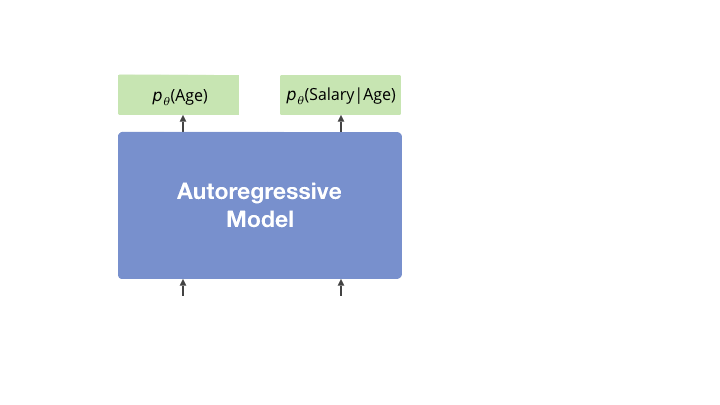
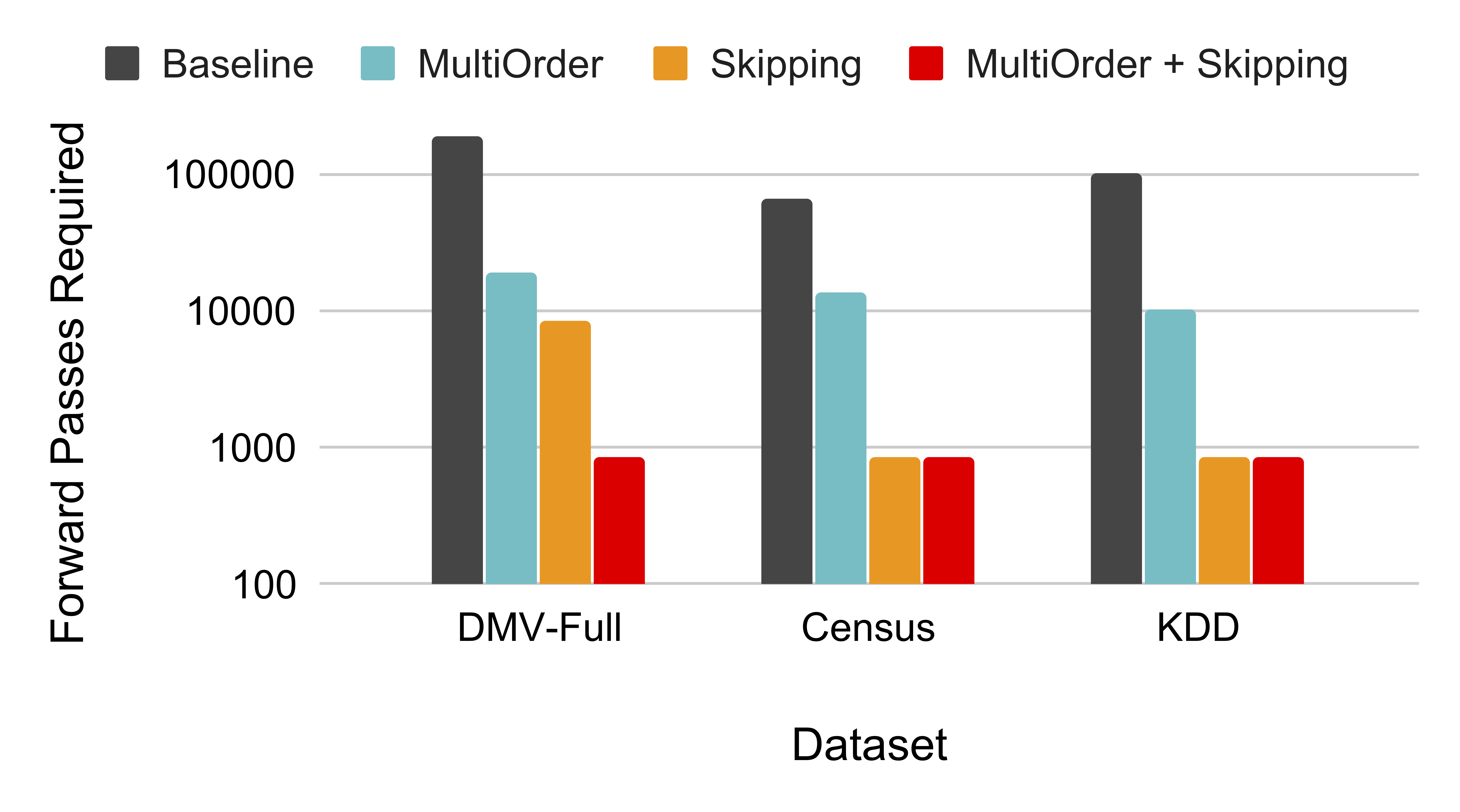 Approximate number of model forward passes required to achieve single-digit inference error at the 99th quantile.
Approximate number of model forward passes required to achieve single-digit inference error at the 99th quantile.